前言

本文同步发表在我的洛谷博客-01 字典树学习笔记。

但由于洛谷不允许在博客中添加外链图片，所以我们建议不要跳转至洛谷以便于获得更好的阅读体验。

Update on 2024.7.13：修正一处错误，感谢 skulker 的指出。

01 字典树

前置知识：字典树。

01 字典树是一种特殊的字典树，它会把数字看作二进制的 $\texttt{01}$ 串存入字符串。

在树上，除了叶子节点外的所有节点都表示一个数的范围。

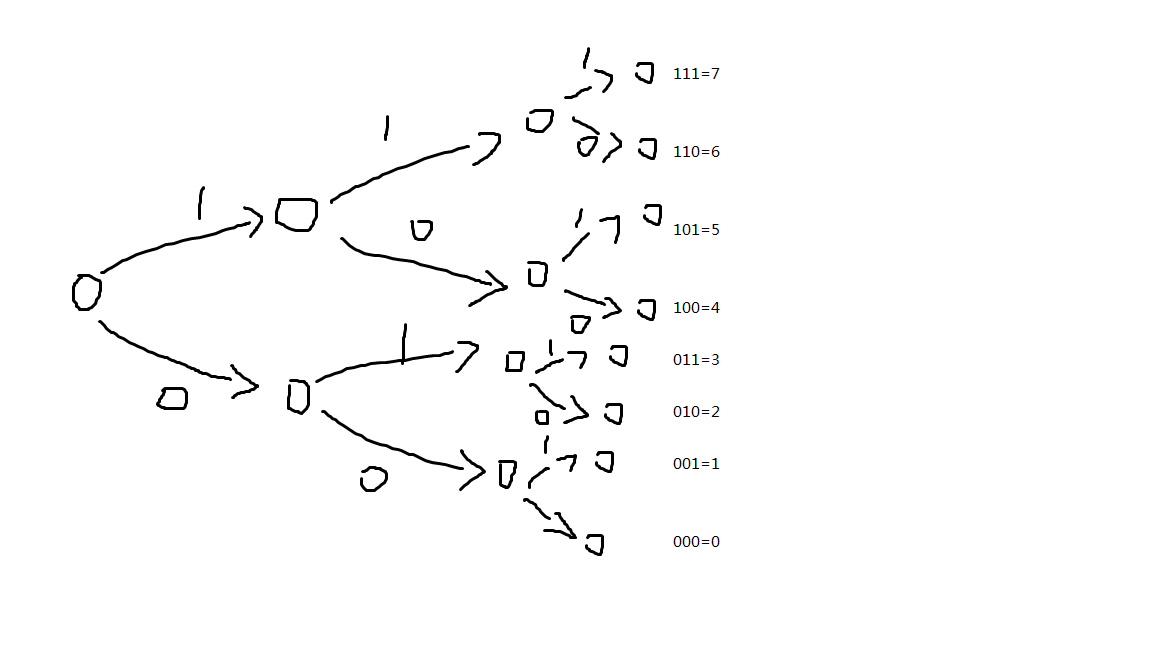
我们在插入元素时，和在字典树中插入元素时类似的。这里不再阐述。

插入示例代码如下：

const int MAXN = 2e6 + 5, MAXL = 31;
int tr[MAXN][2], cnt[MAXN], r = 1;
void insert(int x){
  int u = 1;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (!tr[u][v]){
      tr[u][v] = ++r;
    }
    u = tr[u][v];
    cnt[u]++;
  }
}

如果我们把每个节点表示的数字都存储下来，那么就会是这样：

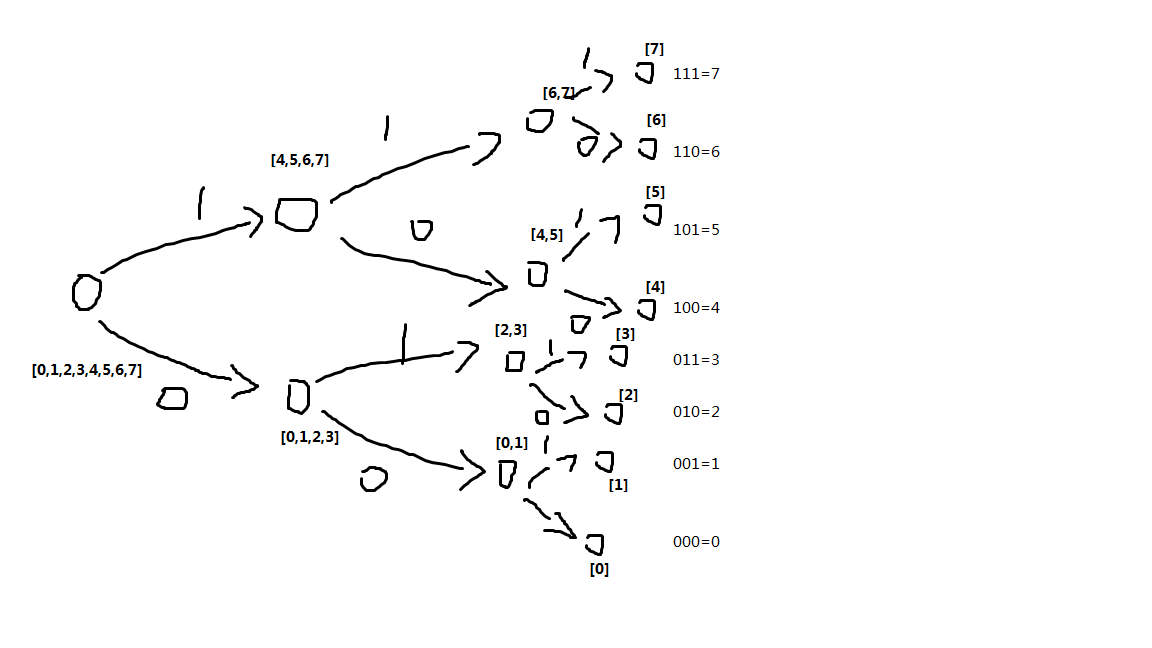
再修改一下，就变成了这样：

[0,7]\to\begin{cases} [4,7]\to\begin{cases} [6,7]\to\begin{cases} [6]\\ [7]\\ \end{cases} \\ [4,5]\to\begin{cases} [4]\\ [5] \end{cases}\\ \end{cases}\\ [0,3]\to\begin{cases} [2,3]\to \begin{cases} [2]\\ [3] \end{cases} \\ [0,1]\to\begin{cases} [0]\\ [1] \end{cases} \end{cases} \end{cases}

那么我们就可以发现：每个节点表示的数字都是一个区间。 $\color{white}{是不是很像线段树？}$

那么 01 字典树能做些什么呢？它通常用来解决一些与位运算有关的问题。具体我们来看题。

当然，我们也可以使用 01 字典树以 $O(\log_2 x)$ 的时间复杂度判断一个数字 $x$ 是否出现过。相比于 map，常数会小很多。

例 1：洛谷 U77096 字典树|the xor largest pair

题意：给定 $n$ 个正整数 $A_1,A_2,\dots,A_n$ ，求出 $\max\limits_{x\in A,y\in A}\{x\oplus y\}$

数据范围： $1\le n\le 10^5,0\le A_i\le 2^{31}$ 。

本题我们就可以使用 01 字典树完成。

首先，对于异或来说， $1\oplus 0=0\oplus 1=1$ 。

那么，如果我们想让这个异或值最大，对于 $a_i$ ，我们选择的匹配的数字的每一位就要尽可能的与 $a_i$ 的对应位不同。

那么，我们在存储时记录下对应位置 $x$ 中 0、1 的是否出现过，查找时尽量匹配与 $a_i$ 对应位不同的数，最后对答案求最大值即可。

参考代码如下：

#include<bits/stdc++.h>

using namespace std;
const int MAXN = 7e6 + 5, MAXL = 31;
int tr[MAXN][2], r = 1, n, a[MAXN];
bool cnt[MAXN];
void insert(int x){
  int u = 1;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (!tr[u][v]){
      tr[u][v] = ++r;
    }
    u = tr[u][v];
    cnt[u] = 1;
  }
}
int find(int x){
  int u = 1, ans = 0;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (tr[u][(v ^ 1)] && cnt[tr[u][v ^ 1]]){
      u = tr[u][(v ^ 1)];
      ans |= ((v ^ 1) << j);
    }else if (tr[u][v] && cnt[tr[u][v]]){
      u = tr[u][v];
      ans |= (v << j);
    }else {
      return ans;
    }
  }
  return ans;
}
int main(){
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
  cin >> n;
  for (int i = 1; i <= n; i++){
    cin >> a[i];
    insert(a[i]);
  }
  long long ans = -1;
  for (int i = 1; i <= n; i++){
    ans = max(ans, 1ll * (a[i] ^ find(a[i])));
  }
  cout << ans;
  return 0;
}

但是，如果这道题还增加了一个操作呢？那么就来到了下一题。

例二：CodeForces-706-D Vasiliy's Multiset

题意：有 $q$ 次询问。初始序列 $A$ 中只有一个数字 $0$ 。每次询问属于以下三种操作之一：
1.+ x 表示将 $x$ 加入序列 $A$ 。
2.- x 表示将 $x$ 从序列 $A$ 中删除。如果序列中有多个 $x$ ，那么只删除一个。
3.? x 表示求出 $\max\limits_{y\in A}\{x\oplus y\}$ 。

对于每次询问 $3$ ，输出一个数表示答案。

数据范围： $1\le q\le 2\times 10^5,0\le A_i\le 10^9$ 。

本题的其他实现与例 1 类似。但是增加了一个删除操作。

我们可以对 cnt 数组进行修改。从记录一个位置是否出现过改为一个位置出现过的次数。

删除操作就只要对对应位置的的出现次数减一即可。

参考代码如下：

#include<bits/stdc++.h>
 
using namespace std;
const int MAXN = 7e6 + 5, MAXL = 31;
int tr[MAXN][2], cnt[MAXN], r = 1;
void insert(int x){
  int u = 1;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (!tr[u][v]){
      tr[u][v] = ++r;
    }
    u = tr[u][v];
    cnt[u]++;
  }
}
int find(int x){
  int u = 1, ans = 0;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (tr[u][(v ^ 1)] && cnt[tr[u][v ^ 1]]){
      u = tr[u][(v ^ 1)];
      ans |= ((v ^ 1) << j);
    }else if (tr[u][v] && cnt[tr[u][v]]){
      u = tr[u][v];
      ans |= (v << j);
    }else {
      return ans;
    }
  }
  return ans;
}
void del(int x){
  int u = 1;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    u = tr[u][v];
    cnt[u]--;
  }
}
int main(){
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
  int q;
  cin >> q;
  insert(0);
  while (q--){
    char s;
    int x;
    cin >> s >> x;
    if (s == '+'){
      insert(x);
    }else if (s == '-'){
      del(x);
    }else {
      cout << (x ^ find(x)) << '\n';
    }
  }
  return 0;
}

例 3：HDU-6955 Xor sum

题意：有 $t$ 组数据，每组数据给定一个长度为 $n$ 的序列 $a$ 。请你找出一个异或和不小于 $k$ 的最短连续子串。

如果有多个满足要求的连续子串，输出左端点最小的。

如果不存在这样的序列，输出 -1。

数据范围： $1\le t\le 100,1\le n\le 10^5,0\le k\le 2^{30},0\le a_i\le 2^{30}$ 。

我们注意到，如果存在一个序列 $a_1,a_2,a_3,a_4$ ，那么有 $a_3\oplus a_4=a_1\oplus a_2\oplus a_3\oplus a_4\oplus a_1\oplus a_2$ 。

也就是说，异或满足类似前缀和的思路。

所以，我们可以对序列 $a$ 求前缀异或和，存储在数组 $b$ 中。

此时，问题就转化为了：求两个数 $l,r$ ，要求 $l$ 和 $r - l + 1$ 都最小，并且满足 $b_r\oplus b_{l-1}\ge k$ 。

现在，来考虑 insert 和 find 函数的实现。

我们可以把 $cnt$ 数组记录的东西修改一下。因为我们要在满足条件的条件下使得在 $r$ 一定的情况下 $l$ 最大，那么我们就可以记录对应位置的 $l$ 的最大值。

insert 函数的实现如下：

void insert(int x, int l){
  int u = 1;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (!tr[u][v]){
      tr[u][v] = ++r;
    }
    u = tr[u][v];
    cnt[u] = max(cnt[u], l);
  }
}

接下来是 find 函数。

首先我们需要让区间异或和 $x\ge k$ ，那么我们就看 $k$ 的其中一个位数是 $0$ 还是 $1$ 。如果这一位是 $1$ ，那么我们在选择数字的时候就只能选择 $0$ 。否则， $0$ 、 $1$ 都可以选择。

如果这一位是 $0$ ，那么对应位是 $1$ 的一定满足答案的要求。此时就可以更新答案。

最后整合输出即可。

完整代码如下：

#include<bits/stdc++.h>

using namespace std;
const int MAXV = 7e6 + 5, MAXL = 31, MAXN = 1e5 + 5;
int n, k, r = 1, t, tr[MAXV][2], a[MAXN], qz[MAXN], cnt[MAXV];
void insert(int x, int l){
  int u = 1;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1;
    if (!tr[u][v]){
      tr[u][v] = ++r;
    }
    u = tr[u][v];
    cnt[u] = max(cnt[u], l);
  }
}
int find(int x){
  int u = 1, ans = 0;
  for (int j = 30; j >= 0; j--){
    int v = (x >> j) & 1, z = (k >> j) & 1;
    if (z){
      u = tr[u][(v ^ 1)];
    }else {
      ans = max(ans, cnt[tr[u][(v ^ 1)]]);
      u = tr[u][v];
    }
  }
  return max(ans, cnt[u]);
}
void Solve(){
  for (int i = 1; i <= r; i++){
    tr[i][0] = tr[i][1] = cnt[i] = 0;
  }
  r = 1;
  cin >> n >> k;
  int ansl = -1, ansr = 1e9;
  for (int i = 1; i <= n; i++){
    cin >> a[i];
    qz[i] = (qz[i - 1] ^ a[i]);
    insert(qz[i - 1], i);
    int x = find(qz[i]);
    if (x > 0 && i - x < ansr - ansl){
      ansl = x, ansr = i;
    }
  }
  
  if (ansl == -1){
    cout << "-1\n";
  }else {
    cout << ansl << ' ' << ansr << '\n';
  }
}
int main(){
  ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
  cin >> t;
  while (t--){
    Solve();
  }
  return 0;
}

例 4：洛谷-P3369 普通平衡树

题意：有 $n$ 次询问，每次询问格式为 op x。具体含义如下：

$op=1$ ：插入数字 $x$ 。
$op=2$ ：删除数字 $x$ 。如果有多个，就只删除一个。
$op=3$ ：询问 $x$ 的排名。一个数的排名为比它小的数字加一。
$op=4$ ：查询排名为 $x$ 的数字。
$op=5$ ：求小于 $x$ 且最大的数。
$op=6$ ：求大于 $x$ 且最小的数。

数据范围： $1\le n\le 10^5,|x|\le 10^7,1\le op\le 6$ 。

虽然这题叫做平衡树，但是我们也可以使用 01 字典树实现。

首先观察到 $x$ 可以为负数，但 01 字典树不能使用负数，所以我们就整体加上偏移量 $10^7$ ，输出的时候再减去 $10^7$ 即可。

操作一二没啥好说的，和上面的一样。

对于操作三，我们发现：如果当前位是 $1$ ，那么当前位是 $0$ 的一定都小于当前数。答案累加即可。

代码如下：

void finda(int x){
  int ans = 0, u = 1;
  for (int j = 25; j >= 0; j--){
    int v = (x >> j) & 1;
    if (v){
      ans += cnt[tr[u][0]];
    }
    u = tr[u][v];
  }
  cout << ans + 1 << '\n';
}

操作四和操作三差不多。代码如下：

void findb(int x){
  int u = 1, ans = 0;
  for (int j = 25; j >= 0; j--){
    if (cnt[tr[u][0]] < x){
      x -= cnt[tr[u][0]];
      u = tr[u][1];
      ans |= (1ll << j);
    }else {
      u = tr[u][0];
    }
  }
  int p = 1e7;
  cout << ans - p << '\n';
}

但是对于操作五和操作六呢？

我们可以发现：比 $x$ 小且最大的数字的排名一定是 $x$ 的排名减一。那么答案就是 findb(finda(x)-1)。

那么操作六也差不多。比 $x$ 大且最小的数字的排名也就是 $x$ 的排名加上 $x$ 的出现次数 $p$ 。那么答案就是 findb(finda(x)+p)。

当然操作五六也可以使用 multiset 进行维护。这里我们不在探讨。

最后，还是希望大家能把上面的四道例题消化好，在 OI 的道路上砥砺前行！

天边的生活の博客

01 字典树学习笔记

前言

01 字典树

例 1：洛谷 U77096 字典树|the xor largest pair

例二：CodeForces-706-D Vasiliy's Multiset

例 3：HDU-6955 Xor sum

例 4：洛谷-P3369 普通平衡树

2023/09/21 图论专题训练