基环树

在树形结构中添加 $1$ 条边形成的图。

分类

1.无向图基环树；
2.内向基环树（每个点的出度均为 $1$ ，如下图所示）；

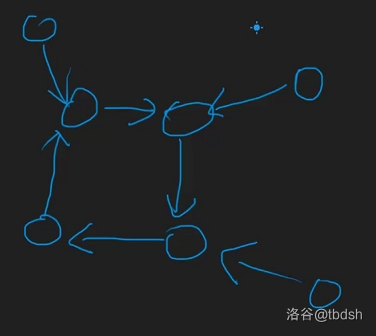
3.外向基环树（每个点的入度均为 $1$）。

找环

方法 1：无向图基环树找环：
1.统计节点的度数 $deg_i$；

2.将度数为 $1$ 的点入队；

3.循环从队头取出结点 $x$，并将 $x$ 的邻接点 $y$ 度数减 $1$；

4.若 $dpg_y=1$，那么 $y$ 入队，重复步骤 2-4；

5.最后 $deg_i>1$ 的点就一定是环上的点。

优点：时间复杂度线性。

缺点：无法知道环上点的顺序。

方法 2：有向图和无向图均适用。

原理：在搜索树中检查一个点 $x$ 的子结点 $y$ 是否深度更浅。
示例代码：

void dfs(int x){
  sd[x] = sd[fa[x]] + 1;
  for (auto v : g[x]){
    if (v == fa[x]){
      continue;
    }
    if (!sd[v]){
      fa[v] = x;
      dfs(v);
    }else if (sd[v] < sd[x]){
      int tmp = x;
      while (tmp != fa[v]){
        vis[tmp] = 1;//点 tmp 在环中
        loop[++id] = tmp//tmp 是环上的第 id 个点
        tmp = fa[tmp];
      }
    }
  }
}

方法 3：tarjan 拓展（适用于无向边）

原理：从环上某个点 $x$ 沿着某个方向到达 $y$，当 $x$ 沿着另一侧到达点 $y$ 时，存在 $dfn_y > dfn_x$。

示例代码：

void dfs(int x){
  dfn[x] = ++cnt;
  for (auto v : g[x]){
    if (v != fa[x]){
      if (!dfn[v]){
        fa[v] = x;
        dfs(v);
      }else if (dfn[v] > dfn[x]){
        int tmp = v;
        while (tmp != fa[x]){//注意这里和方法 2 的区别
          vis[tmp] = 1;
          loop[++id] = tmp;
          tmp = fa[tmp];
        }
      }
    }
  }
}

基环树的使用技巧

1.把环当做根结点，分成环上的点和环上点的子树分别处理；

2.把环断开，变成一棵树来处理。

P2607：
1.每个点向其唯一憎恨的点不能同时选择；

2.连无向边，得到基环树；

3.任意枚举一条环上的边及其端点 $x,y$；

4.分别从 $x,y$ 跑一遍树形 DP 即可（类似 P1352 没有上司的舞会）。

P4381：咕咕咕