前言

我太菜了，板子调了一晚上没看出线段树写错了。

概念

自 OI Wiki 搬运。
重儿子：子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

轻儿子：一个结点所有子结点除了重儿子外的所有节点。

重边：从这个结点到重子节点的边。

轻边：从这个结点到其他轻子节点的边。

重链：若干条首尾衔接的重边构成。

例如：

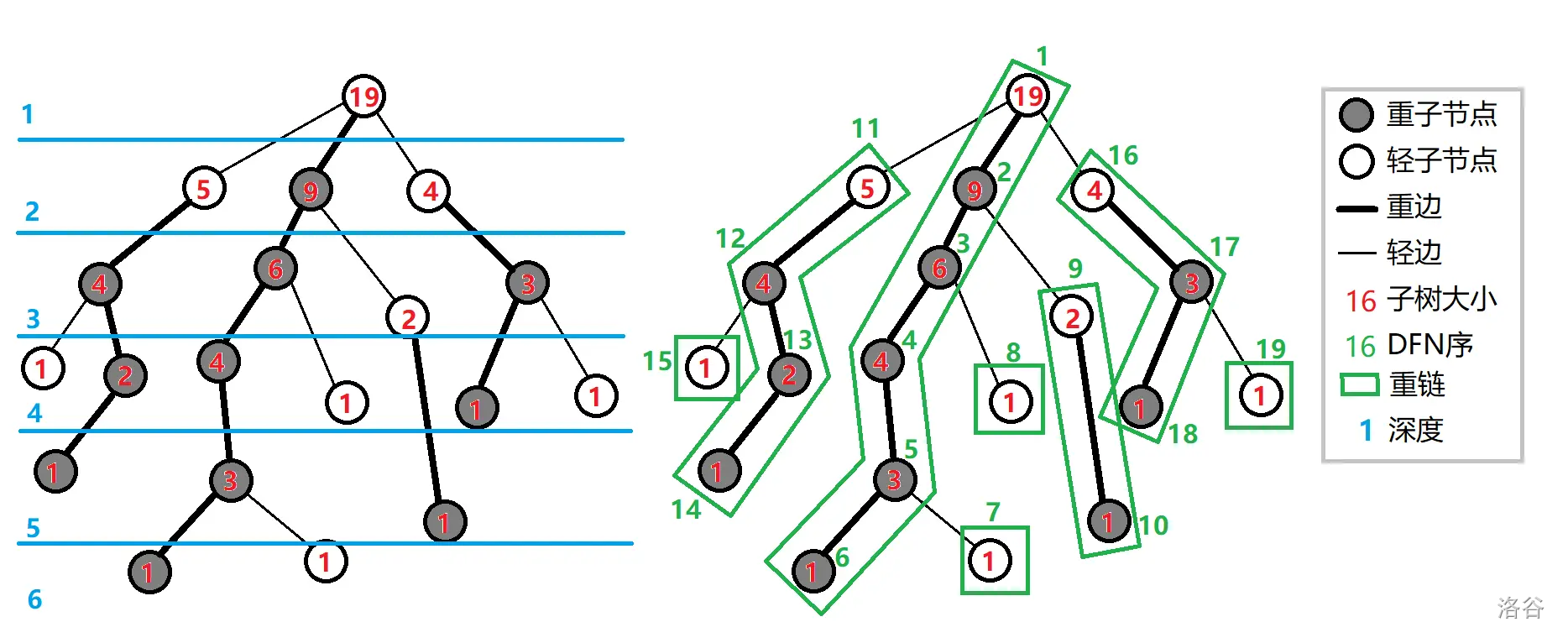
实现

重链剖分（下简称树剖）主要需要两次 DFS。

第一次 DFS 记录每个节点的父节点 $fa_i$、深度 $sd_i$，子树大小 $sz_i$，重儿子 $son_i$。

实现代码如下：

void dfs1(int x, int f){
  fa[x] = f;
  sd[x] = sd[f] + 1;
  sz[x]++;
  for (auto v : g[x]){
    if (v != f){
      dfs1(v, x);
      sz[x] += sz[v];
      if (sz[v] > sz[son[x]]){
        son[x] = v;
      }
    }
  }
}

dfs1(root, 0); //调用函数。

第二次 DFS 需要将整棵树分为不超过 $O(\log n)$ 条链，记录所有节点所在链的链头 $top_i$，求出所有节点在 DFS 序上的位置 $id_i$。

注意，我们在进行 DFS 的时候优先向下遍历重儿子，这样可以保证子树的所有节点在 DFS 序上的位置是连续的。

实现代码如下：

void dfs2(int x, int f){
  id[x] = ++cnt;
  a[cnt] = w[x];
  top[x] = f;
  if (!son[x]){
    return ;
  }
  dfs2(son[x], f);
  for (auto v : g[x]){
    if (v == fa[x] || v == son[x]){
      continue;
    }
    dfs2(v, v);
  }
}

那么现在，我们就完成了树剖的所有内容！学习笔记到此结束！

那么，我们来看几道题。

洛谷 P3384 【模板】重链剖分/树链剖分

题目大意：

已知一棵包含 $N$ 个结点且根为 $R$ 的树（连通且无环），每个节点上包含一个数值，需要进行 $M$ 次操作。每次操作是以下操作之一：

• 1 x y z，表示将树从 $x$ 到 $y$ 结点最短路径上所有节点的值都加上 $z$。

• 2 x y，表示求树从 $x$ 到 $y$ 结点最短路径上所有节点的值之和。

• 3 x z，表示将以 $x$ 为根节点的子树内所有节点值都加上 $z$。

• 4 x 表示求以 $x$ 为根节点的子树内所有节点值之和。

**所有答案需要对常数 $P$ 取模。

数据范围：

$1\le N \leq {10}^5$，$1\le M \leq {10}^5$，$1\le R\le N$，$1\le P \le 2^{31}-1$。所有输入的数均在 int 范围内。

我们已经完成了树剖的操作。由于此时同一子树上的所有节点编号是连续的，那么我们就可以直接建线段树了！

建线段树的部分我们不在赘述。但是在此我们来看看操作 $1$ 和操作 $2$ 的具体实现。

由于这两个点不一定在同一条链上，所以不好解决。但我们可以用求 LCA 的思想来求。

在向上跳的过程中，如果当前节点在重链上，向上跳到重链顶端的上一个点，如果当前节点不在重链上，那么向上跳一个节点。如此直到两节点相同。沿途更新/查询区间信息。

对于每次操作来说，最多经过 $O(\log n)$ 条链，线段树查询/修改的时间复杂度为 $O(\log n)$。因此一次操作的时间复杂度为 $O(\log^2 n)$。

那么本题最终的完整代码就长这样：Link。

未完待续....