圆方树

基础概念

割点：无向图中，若删除点 $x$ 及其连边，连通块变多，那么 $x$ 为割点。

点双连通：若点对 $(x,y)$ 删除任意非 $x$ 且非 $y$ 结点后，$x$ 和 $y$ 仍然联通，则称 $x$ 和 $y$ 点双联通。

点双联通子图：若无向图中的一个子图 $G$，满足 $G$ 中任意 $2$ 点都是点双联通的，那么 $G$ 为原图的点双联通子图。

点双联通分量：无向图中的极大点双连通子图称为点双联通分量（V-DCC）。

Tips：点双联通不具有传递性，边双连通具有传递性。

反例：

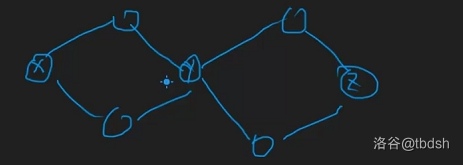
该图中点对 $(x,y)$ 点双联通，点对 $(y,z)$ 点双联通，但删去点 $y$ 后点 $(x,z)$ 不点双联通。

性质

1.无向图至少有 $3$ 个点，才可能有割点。

2.dfs 搜索树中的根节点的子结点数 $x\ge2$ 时才可能是割点。

3.$1$ 个割点可能在多个点双中。

4.点双里面可能有多个割点

圆方树

将无向图转化为树形结构，解决“必经点”问题的数据结构。

目标：构建一棵树，树上 $2$ 点路径上的点都是原图的必经点。

在圆方树中，我们定义：

• 圆点：原无向图 $G$ 中的点，仍然保留在圆方树中，称之为圆点。
• 方点：将每一个点双连通分量新建一个“方点”。
• 树边：每个方点向对应的点双内的圆点连边。

基本性质

1.令 $x$ 表示圆方树中的总点数，$n$ 表示原图点数，$t$ 表示点双个数，有 $x=n+t$ 且点数上限 $x\ge2\times n-1$。

2.圆点是被方点隔开的，一条边的两个端点一定是圆点和方点。

3.圆点的度数就是包含该点的点双个数。

4.圆方树删除点 $x$ 后剩余节点的连通性与原图中删除 $x$ 之后的连通性等价。

5.原图中 $x$ 到 $y$ 的路径的必经点就是圆方树上 $x$ 到 $y$ 经过的所有圆点。

6.圆点为割点时才可能有超过 $1$ 个儿子结点。

核心代码

void dfs(int x, int fa){
  dfn[x] = low[x] = ++cnt;
  st.push(x);
  for (auto v : g[x]){
    if (!dfn[v]){
      dfs(v, x);
      low[x] = min(low[x], low[v]);
      if (low[v] >= dfn[x]){
        yf++;
        while (1){
          int t = st.top();
          st.pop();
          tr[yf].push_back(t);
          tr[t].push_back(yf);
          if (t == v){
            break;
          }
        }
        tr[x].push_back(yf);
        tr[yf].push_back(x);
      }
    }else if (v != fa){
      low[x] = min(low[x], dfn[v]);
    }
  }
}